The guy in the cubicle next to me is showing signs of leaving work later than me again. Which of course makes him a better human being than me, again. This cannot stand! Lee, if you’re reading this, you’re going down. Today, I stay till midnight! Dinner be damned; I’m going to eat my desk if I have to.
Author: Tal Yarkoni
specificity statistics for ROI analyses: a simple proposal
The brain is a big place. In the context of fMRI analysis, what that bigness means is that a typical 3D image of the brain might contain anywhere from 50,000 – 200,000 distinct voxels (3D pixels). Any of those voxels could theoretically show meaningful activation in relation to some contrast of interest, so the only way to be sure that you haven’t overlooked potentially interesting activations is to literally test every voxel (or, given some parcellation algorithm, every region).
Unfortunately, the problem that approach raises–which I’ve discussed in more detail here–is the familiar one of multiple comparisons: If you’re going to test 100,000 locations, it’s not really fair to test each one at the conventional level of p < .05, because on average, you’ll get about 5,000 statistically significant results just by chance that way. So you need to do something to correct for the fact that you’re running thousands of tests. The most common approach is to simply make the threshold for significance more conservative–for example, by testing at p < .0001 instead of p < .05, or by using some combination of intensity and cluster extent thresholds (e.g., you look for 20 contiguous voxels that are all significant at, say, p < .001) that’s supposed to guarantee a cluster-wise error rate of .05.
There is, however, a natural tension between false positives and false negatives: When you make your analysis more conservative, you let fewer false positives through the filter, but you also keep more of the true positives out. A lot of fMRI analysis really just boils down to walking a very thin line between running overconservative analyses that can’t detect anything but the most monstrous effects, and running overly liberal analyses that lack any real ability to distinguish meaningful signals from noise. One very common approach that fMRI researchers have adopted in an effort to optimize this balance is to use complementary hypothesis-driven and whole-brain analyses. The idea is that you’re basically carving the brain up into two separate search spaces: One small space for which you have a priori hypotheses that can be tested using a small number of statistical comparisons, and one much larger space (containing everything but the a priori space) where you continue to use a much more conservative threshold.
For example, if I believe that there’s a very specific chunk of right inferotemporal cortex that’s specialized for detecting clown faces, I can focus my hypothesis-testing on that particular region, without having to pretend that all voxels are created equal. So I delineate the boundaries of a CRC (Clown Representation Cortex) region-of-interest (ROI) based on some prior criteria (e.g., anatomy, or CRC activation in previous studies), and then I can run a single test at p < .05 to test my hypothesis, no correction needed. But to ensure that I don’t miss out on potentially important clown-related activation elsewhere in the brain, I also go ahead and run an additional whole-brain analysis that’s fully corrected for multiple comparisons. By coupling these two analyses, I hopefully get the best of both worlds. That is, I combine one approach (the ROI analysis) that maximizes power to test a priori hypotheses at the cost of an inability to detect effects in unexpected places with another approach (the whole-brain analysis) that has a much more limited capacity to detect effects in both expected and unexpected locations.
This two-pronged strategy is generally a pretty successful one, and I’d go so far as to say that a very large minority, if not an outright majority, of fMRI studies currently use it. Used wisely, I think it’s really an invaluable strategy. There is, however, one fairly serious and largely unappreciated problem associated with the incautious application of this approach. It has to do with claims about the specificity of activation that often tend to accompany studies that use a complementary ROI/whole-brain strategy. Specifically, a pretty common pattern is for researchers to (a) confirm their theoretical predictions by successfully detecting activation in one or more a priori ROIs; (b) identify few if any whole-brain activations; and consequently, (c) conclude that not only were the theoretical predictions confirmed, but that the hypothesized effects in the a priori ROIs were spatially selective, because a complementary whole-brain analysis didn’t turn up much (if anything). Or, to put it in less formal terms, not only were we right, we were really right! There isn’t any other part of the brain that shows the effect we hypothesized we’d see in our a priori ROI!
The problem with this type of inference is that there’s usually a massive discrepancy in the level of power available to detect effects in a priori ROIs versus the rest of the brain. If you search at p < .05 within some predetermined space, but at only p < .0001 everywhere else, you’re naturally going to detect results at a much lower rate everywhere else. But that’s not necessarily because there wasn’t just as much to look at everywhere else; it could just be because you didn’t look very carefully. By way of analogy, if you’re out picking berries in the forest, and you decide to spend half your time on just one bush that (from a distance) seemed particularly berry-full, and the other half of your time divided between the other 40 bushes in the area, you’re not really entitled to conclude that you picked the best bush all along simply because you came away with a relatively full basket. Had you done a better job checking out the other bushes, you might well have found some that were even better, and then you’d have come away carrying two baskets full of delicious, sweet, sweet berries.
Now, in an ideal world, we’d solve this problem by simply going around and carefully inspecting all the berry bushes, until we were berry, berry sure really convinced that we’d found all of the best bushes. Unfortunately, we can’t do that, because we’re out here collecting berries on our lunch break, and the boss isn’t paying us to dick around in the woods. Or, to return to fMRI World, we simply can’t carefully inspect every single voxel (say, by testing it at p < .05), because then we’re right back in mega-false-positive-land, which we’ve already established as a totally boring place we want to avoid at all costs.
Since an optimal solution isn’t likely, the next best thing is to figure out what we can do to guard against careless overinterpretation. Here I think there’s actually a very simple, and relatively elegant, solution. What I’ve suggested when I’ve given recent talks on this topic is that we mandate (or at least, encourage) the use of what you could call a specificity statistic (SS). The SS is a very simple measure of how specific a given ROI-level finding is; it’s just the proportion of voxels that are statistically significant when tested at the same level as the ROI-level effects. In most cases, that’s going to be p < .05, so the SS will usually just be the proportion of all voxels anywhere in the brain that are activated at p < .05.
To see why this is useful, consider what could no longer happen: Researchers would no longer be able to (inadvertently) capitalize on the fact that the one or two regions they happened to define as a priori ROIs turned up significant effects when no other regions did in a whole-brain analysis. Suppose that someone reports a finding that negative emotion activates the amygdala in an ROI analysis, but doesn’t activate any other region in a whole-brain analysis. (While I’m pulling this particular example out of a hat here, I feel pretty confident that if you went and did a thorough literature review, you’d find at least three or four studies that have made this exact claim.) This is a case where the SS would come in really handy. Because if the SS is, say, 26% (i.e., about a quarter of all voxels in the brain are active at p < .05, even if none survive full correction for multiple comparisons), you would want to draw a very different conclusion than if it was just 4%. If fully a quarter of the brain were to show greater activation for a negative-minus-neutral emotion contrast, you wouldn’t want to conclude that the amygdala was critically involved in negative emotion; a better interpretation would be that the researchers in question just happened to define an a priori region that fell within the right quarter of the brain. Perhaps all that’s happening is that negative emotion elicits a general increase in attention, and much of the brain (including, but by no means limited to, the amygdala) tends to increase activation correspondingly. So as a reviewer and reader, you’d want to know how specific the reported amygdala activation really is*. But in the vast majority of papers, you currently have no way of telling (and the researchers probably don’t even know the answer themselves!).
The principal beauty of this statistic lies in its simplicity: It’s easy to understand, easy to calculate, and easy to report. Ideally, researchers would report the SS any time ROI analyses are involved, and would do it for every reported contrast. But at minimum, I think we should all encourage each other (and ourselves) to report such a statistic any time we’re making a specificity claim about ROI-based results. In other words,if you want to argue that a particular cognitive function is relatively localized to the ROI(s) you happened to select, you should be required to show that there aren’t that many other voxels (or regions) that show the same effect when tested at the liberal threshold you used for the ROI analysis. There shouldn’t be an excuse for not doing this; it’s a very easy procedure for researchers to implement, and an even easier one for reviewers to demand.
* An alternative measure of specificity would be to report the percentile ranking of all of the voxels within the ROI mask relative to all other individual voxels. In the above example, you’d assign very different interpretations depending on whether the amygdala was in the 32nd or 87th percentile of all voxels, when ordered according to the strength of the effect for the negative – neutral contrast.
a well-written mainstream article on fMRI?!
Craig Bennett, of prefrontal.org and dead salmon fame, links to a really great Science News article on the promises and pitfalls of fMRI. As Bennett points out, the real gem of the article is the “quote of the week” from Nikos Logethetis (which I won’t spoil for you here; you’ll have to do just a little more work to get to it). But the article is full of many other insightful quotes from fMRI researchers, and manages to succinctly and accurately describe a number of recent controversies in the fMRI literature without sacrificing too much detail. Usually when I come across a mainstream article on fMRI, I pre-emptively slap the screen a few times before I start reading, because I know I’m about to get angry. Well, I did that this time too, so my hand hurts per usual, but at least this time I feel pretty good about it. Kudos to Laura Sanders for writing one of the best non-technical accounts I’ve seen of the current state of fMRI research (and that, unlike a number of other articles in this vein, actually ends on a balanced and optimistic note).
every day is national lab day
This week’s issue of Science has a news article about National Lab Day, a White House-supported initiative to pair up teachers and scientists in an effort to improve STEM education nation-wide. As the article notes, National Lab Day is a bit of a misnomer, seeing as the goal is to encourage a range of educational activities over the next year or so. That’s a sentiment I can appreciate; why pick just one national lab day when you can have ALL OF THEM.
In any case, if you’re a scientist, you can sign up simply by giving away all of your deepest secrets and best research ideas providing your contact information and describing your academic background. I’m not really sure what happens after that, but in theory, at some point you’re supposed to wind up in a K-12 classroom demonstrating what you do and why it’s cool, which I guess could involve activities like pulling french fries out of burning oil with your bare hands, or applying TMS to 3rd graders’ foreheads, or other things of that nature. Of course, you can’t really bring an fMRI scanner into a classroom (though I suppose you could bring a classroom to an fMRI scanner), so I’m not really sure what I’ll do if anyone actually contacts me and asks me to come visit their classroom. I guess there’s always videos of lesion patients and the Muller-Lyer illusion, right?
building a cumulative science of human brain function at CNS
Earlier today, I received an email saying that a symposium I submitted for the next CNS meeting was accepted for inclusion in the program. I’m pretty excited about this; I think the topic of the symposium is a really important one, and this will be a great venue to discuss some of the relevant issues. The symposium is titled “Toward a cumulative science of human brain function”, which is a pretty good description of its contents. Actually, I stole borrowed that title from one of the other speakers (Tor Wager); originally, the symposium was going to be called something like “Cognitive Neuroscience would Suck Less if we all Pooled our Findings Together Instead of Each Doing our own Thing.” In hindsight, I think title theft was the right course of action. Anyway, with the exception of my own talk, which is assured of being perfectly mediocre, the line-up is really stellar; the other speakers are David Van Essen, Tor Wager (my current post-doc advisor), and Russ Poldrack, all of whom do absolutely fantastic research, and give great talks to boot. Here’s the symposium abstract:
This symposium is designed to promote development of a cumulative science of human brain function that advances knowledge through formal synthesis of the rapidly growing functional neuroimaging literature. The first speaker (Tal Yarkoni) will motivate the need for a cumulative approach by highlighting several limitations of individual studies that can only be overcome by synthesizing the results of multiple studies. The second speaker (David Van Essen) will discuss the basic tools required in order to support formal synthesis of multiple studies, focusing particular attention on SumsDB, a massive database of functional neuroimaging data that can support sophisticated search and visualization queries. The third and fourth speakers will discuss two different approaches to combining and filtering results from multiple studies. Tor Wager will review state-of-the-art approaches to meta-analysis of fMRI data, providing empirical examples of the power of meta-analysis to both validate and disconfirm widely held views of brain organization. Russell Poldrack will discuss a novel taxonomic approach that uses collaboratively annotated meta-data to develop formal ontologies of brain function. Collectively, these four complementary talks will familiarize the audience with (a) the importance of adopting cumulative approaches to functional neuroimaging data; (b) currently available tools for accessing and retrieving information from multiple studies; and (c) state-of-the-art techniques for synthesizing the results of different functional neuroimaging studies into an integrated whole.
Anyway, I think it’ll be a really interesting set of talks, so if you’re at CNS next year, and find yourself hanging around at the convention center for half a day (though why you’d want to do that is beyond me, given that the conference is in MONTREAL), please check it out!
solving the file drawer problem by making the internet the drawer
UPDATE 11/22/2011 — Hal Pashler’s group at UCSD just introduced a new website called PsychFileDrawer that’s vastly superior in every way to the prototype I mention in the post below; be sure to check it out!
Science is a difficult enterprise, so scientists have many problems. One particularly nasty problem is the File Drawer Problem. The File Drawer Problem is actually related to another serious scientific problem known as the Desk Problem. The Desk Problem is that many scientists have messy desks covered with overflowing stacks of papers, which can make it very hard to find things on one’s desk–or, for that matter, to clear enough space to lay down another stack of papers. A common solution to the Desk Problem is to shove all of those papers into one’s file drawer. Which brings us to the the File Drawer Problem. The File Drawer Problem refers to the fact that, eventually, even the best-funded of scientists run out of room in their file drawers.
Ok, so that’s not exactly right. What the file drawer problem–a term coined by Robert Rosenthal in a seminal 1979 article–really refers to is the fact that null results tend to go unreported in the scientific literature at a much higher rate than positive findings, because journals don’t like to publish papers that say “we didn’t find anything”, and as a direct consequence, authors don’t like to write papers that say “journals won’t want to publish this”.
Because of this blatant prejudice systematic bias against null results, the eventual resting place of many a replication failure is its author’s file drawer. The reason this is a problem is that, over the long term, if only (or mostly) positive findings ever get published, researchers can get a very skewed picture of how strong an effect really is. To illustrate, let’s say that Joe X publishes a study showing that people with lawn gnomes in their front yards tend to be happier than people with no lawn gnomes in their yards. Intuitive as that result may be, someone is inevitably going to get the crazy idea that this effect is worth replicating once or twice before we all stampede toward Home Depot or the Container Store with our wallets out (can you tell I’ve never bought a lawn gnome before?). So let’s say Suzanna Y and Ramesh Z each independently try to replicate the effect in their labs (meaning, they command their graduate students to do it). And they find… nothing! No effect. Turns out, people with lawn gnomes are just as miserable as the rest of us. Well, you don’t need a PhD in lawn decoration to recognize that Suzanna Y and Ramesh Z are not going to have much luck publishing their findings in very prestigious journals–or for that matter, in any journals. So those findings get buried into their file drawers, where they will live out the rest of their days with very sad expressions on their numbers.
Now let’s iterate this process several times. Every couple of years, some enterprising young investigator will decide she’s going to try to replicate that cool effect from 2009, since no one else seems to have bothered to do it. This goes on for a while, with plenty of null results, until eventually, just by chance, someone gets lucky (if you can call a false positive lucky) and publishes a successful replication. And also, once in a blue moon, someone who gets a null result actually bothers to forces their graduate student to write it up, and successfully gets out a publication that very carefully explains that, no, Virginia, lawn gnomes don’t really make you happy. So, over time, a small literature on the hedonic effects of lawn gnomes accumulates.
Eventually, someone else comes across this small literature and notices that it contains “mixed findings”, with some studies finding an effect, and others finding no effect. So this special someone–let’s call them the Master of the Gnomes–decides to do a formal meta-analysis. (A meta-analysis is basically just a fancy way of taking a bunch of other people’s studies, throwing them in a blender, and pouring out the resulting soup into a publication of your very own.) Now you can see why the failure to publish null results is going to be problematic: What the Master of the Gnomes doesn’t know about, the Master of the Gnomes can’t publish about. So any resulting meta-analytic estimate of the association between lawn gnomes and subjective well-being is going to be biased in the positive directio. That is, there’s a good chance that the meta-analysis will end up saying lawn gnomes make people very happy,when in reality lawn gnomes only make people a little happy, or don’t make people happy at all.
There are lots of ways to try to get around the file drawer problem, of course. One approach is to call up everyone you know who you think might have ever done any research on lawn gnomes and ask if you could take a brief peek into their file drawer. But meta-analysts are often very introverted people with no friends, so they may not know any other researchers. Or they might be too shy to ask other people for their data. And then too, some researchers are very protective of their file drawers, because in some cases, they’re hiding more than just papers in there. Bottom line, it’s not always easy to identify all of the null results that are out there.
A very different way to deal with the file drawer problem, and one suggested by Rosenthal in his 1979 article, is to compute a file drawer number, which is basically a number that tells you how many null results that you don’t know about would have to exist in people’s file drawers before the meta-analytic effect size estimate was itself rendered null. So, for example, let’s say you do a meta-analysis of 28 studies, and find that your best estimate, taking all studies into account, is that the standardized effect size (Cohen’s d) is 0.63, which is quite a large effect, and is statistically different from 0 at, say, the p < .00000001 level. Intuitively, that may seem like a lot of zeros, but being a careful methodologist, you decide you’d like a more precise definition of “a lot”. So you compute the file drawer number (in one of its many permutations), and it turns out that there would have to be 4,640,204 null results out there in people’s file drawers before the meta-analytic effect size became statistically non-significant. That’s a lot of studies, and it’s doubtful that there are even that many people studying lawn gnomes, so you can probably feel comfortable that there really is an association there, and that it’s fairly large.
The problem, of course, is that it doesn’t always turn out that way. Sometimes you do the meta-analysis and find that your meta-analytic effect is cutting it pretty close, and that it would only take, say, 12 null results to render the effect non-significant. At that point, the file drawer N is no help; no amount of statistical cleverness is going to give you the extrasensory ability to peer into people’s file drawers at a distance. Moreover, even in cases where you can feel relatively confident that there couldn’t possibly be enough null results out there to make your effect go away entirely, it’s still possible that there are enough null results out there to substantially weaken it. Generally speaking, the file drawer N is a number you compute because you have to, not because you want to. In an ideal world, you’d always have all the information readily available at your fingertips, and all that would be left for you to do is toss it all in the blender and hit “liquify” “meta-analyze”. But of course, we don’t live in an ideal world; we live in a horrible world full of things like tsunamis, lip syncing, and publication bias.
This brings me, in a characteristically long-winded way, to the point of this post. The fact that researchers often don’t have access to other researchers’ findings–null result or not–is in many ways a vestige of the fact that, until recently, there was no good way to rapidly and easily communicate one’s findings to others in an informal way. Of course, the telephone has been around for a long time, and the postal service has been around even longer. But the problem with telling other people what you found on the telephone is that they have to be listening, and you don’t really know ahead of time who’s going to want to hear about your findings. When Rosenthal was writing about file drawers in the 80s, there wasn’t any bulletin board where people could post their findings for all to see without going to the trouble of actually publishing them, so it made sense to focus on ways to work around the file drawer problem instead of through it.
These days, we do have a bulletin board where researchers can post their null results: The internet. In theory, an online database of null results presents an ideal solution to the file drawer problem: Instead of tossing their replication failures into a folder somewhere, researchers could spend a minute or two entering just a minimal amount of information into an online database, and that information would then live on in perpetuity, accessible to anyone else who cared to come along and enter the right keyword into the search box. Such a system could benefit everyone involved: researchers who ended up with unpublishable results could salvage at least some credit for their efforts, and ensure that their work wasn’t entirely lost to the sands of time; prospective meta-analysts could simplify the task of hunting down relevant findings in unlikely places; and scientists contemplating embarking on a new line of research that built heavily on an older finding could do a cursory search to see if other people had already tried (and failed) to replicate the foundational effect.
Sounds good, right? At least, that was my thought process last year, when I spent some time building an online database that could serve as this type of repository for null (and, occasionally, not-null) results. I got a working version up and running at failuretoreplicate.com, and was hoping to spend some time begging people to use it trying to write it up as a short paper, but then I started sinking into the quicksand of my dissertation, and promptly forgot about it. What jogged my memory was this post a couple of days ago, which describes a database, called the Negatome, that contains “a collection of protein and domain (functional units of proteins) pairs thatare unlikely to be engaged in direct physical interactions”. This isn’t exactly the same thing as a database of null results, and is in a completely different field, but it was close enough to rekindle my interest and motivate me to dust off the site I built last year. So now the site is here, and it’s effectively open for business.
I should confess up front that I don’t harbor any great hopes of this working; I suspect it will be quite difficult to build the critical mass needed to make something like this work. Still, I’d like to try. The site is officially in beta, so stuff will probably still break occasionally, but it’s basically functional. You can create an account instantly and immediately start adding studies; it only takes a minute or two per study. There’s no need to enter much in the way of detail; the point isn’t to provide an alternative to peer-reviewed publication, but rather to provide a kind of directory service that researchers could use as a cursory tool for locating relevant information. All you have to do is enter a brief description of the effect you tried to replicate, an indication of whether or not you succeeded, and what branch of psychology the effect falls under. There are plenty of other fields you can enter (e.g., searchable tags, sample sizes, description of procedures, etc.), but they’re almost all optional. The goal is really to make this as effortless as possible for people to use, so that there is no virtually no cost to contributing.
Anyway, right now there’s nothing on the site except a single lonely record I added in order to get things started. I’d be very grateful to anyone who wants to help this project off the ground by adding a study or two. There are full editing and deletion capabilities, so you can always delete anything you add later on if you decide you don’t want to share after all. My hope is that, given enough community involvement and a large enough userbase, this could eventually become a valuable resource psychologists could rely on when trying to establish how likely a finding is to replicate, or when trying to identify relevant studies to include in meta-analyses. You do want to help figure out what effect those sneaky, sneaky lawn gnomes have on our collective mental health, right?
Ioannidis on effect size inflation, with guest appearance by Bozo the Clown
Andrew Gelman posted a link on his blog today to a paper by John Ioannidis I hadn’t seen before. In many respects, it’s basically the same paper I wrote earlier this year as a commentary on the Vul et al “voodoo correlations” paper (the commentary was itself based largely on an earlier chapter I wrote with my PhD advisor, Todd Braver). Well, except that the Ioannidis paper came out a year earlier than mine, and is also much better in just about every respect (more on this below).
What really surprises me is that I never came across Ioannidis’ paper when I was doing a lit search for my commentary. The basic point I made in the commentary–which can be summarized as the observation that low power coupled with selection bias almost invariably inflates significant effect sizes–is a pretty straightforward statistical point, so I figured that many people, and probably most statisticians, were well aware of it. But no amount of Google Scholar-ing helped me find an authoritative article that made the same point succinctly; I just kept coming across articles that made the point tangentially, in an off-hand “but of course we all know we shouldn’t trust these effect sizes, because…” kind of way. So I chalked it down as one of those statistical factoids (of which there are surprisingly many) that live in the unhappy land of too-obvious-for-statisticians-to-write-an-article-about-but-not-obvious-enough-for-most-psychologists-to-know-about. And so I just went ahead and wrote the commentary in a non-technical way that I hoped would get the point across intuitively.
Anyway, after the commentary was accepted, I sent a copy to Andrew Gelman, who had written several posts about the Vul et al controversy. He promptly send me back a link to this paper of his, which basically makes the same point about sampling error, but with much more detail and much better examples than I did. His paper also cites an earlier article in American Scientist by Wainer, which I also recommend, and again expresses very similar ideas. So then I felt a bit like a fool for not stumbling across either Gelman’s paper or Wainer’s earlier. And now that I’ve read Ioannidis’ paper, I feel even dumber, seeing as I could have saved myself a lot of trouble by writing two or three paragraphs and then essentially pointing to Ioannidis’ work. Oh well.
That all said, it wasn’t a complete loss; I still think the basic point is important enough that it’s worth repeating loudly and often, no matter how many times it’s been said before. And I’m skeptical that many fMRI researchers would have appreciated the point otherwise, given that none of the papers I’ve mentioned were published in venues fMRI researchers are likely to read regularly (which is presumably part of the reason I never came across them!). Of course, I don’t think that many people who do fMRI research actually bothered to read my commentary, so it’s questionable whether it had much impact anyway.
At any rate, the Ioannidis paper makes a number of points that my paper didn’t, so I figured I’d talk about them a bit. I’ll start by revisiting what I said in my commentary, and then I’ll tell you why you should read Ioannidis’ paper instead of mine.
The basic intuition can be captured as follows. Suppose you’re interested in the following question: Do clowns suffer depression at a higher rate than us non-comical folk do? You might think this is a contrived (to put it delicately) question, but I can assure you it has all sorts of important real-world implications. For instance, you wouldn’t be so quick to book a clown for your child’s next birthday party if you knew that The Great Mancini was going to be out in the parking lot half an hour later drinking cheap gin out of a top hat. If that example makes you feel guilty, congratulations: you’ve just discovered the translational value of basic science.
Anyway, back to the question, and how we’re going to answer it. You can’t just throw a bunch of clowns and non-clowns in a room and give them a depression measure. There’s nothing comical about that. What you need to do, if you’re rigorous about it, is give them multiple measures of depression, because we all know how finicky individual questionnaires can be. So the clowns and non-clowns each get to fill out the Beck Depression Inventory (BDI), the Center for Epidemiologic Studies Depression Scale, the Depression Adjective Checklist, the Zung Self-Rating Depression Scale (ZSRDS), and, let’s say, six other measures. Ten measures in all. And let’s say we have 20 individuals in each group, because that’s all I personally a cash-strapped but enthusiastic investigator can afford. After collecting the data, we score the questionnaires and run a bunch of t-tests to determine whether clowns and non-clowns have different levels of depression. Being scrupulous researchers who care a lot about multiple comparisons correction, we decide to divide our critical p-value by 10 (the dreaded Bonferroni correction, for 10 tests in this case) and test at p < .005. That’s a conservative analysis, of course; but better safe than sorry!
So we run our tests and get what look like mixed results. Meaning, we get statistically significant positive correlations between clown-dom status and depression for 2 measures–the BDI and Zung inventories–but not for the other 8 measures. So that’s admittedly not great; it would have been better if all 10 had come out right. Still, it at least partially supports our hypothesis: Clowns are fucking miserable! And because we’re already thinking ahead to how we’re going to present these results when they (inevitably) get published in Psychological Science, we go ahead and compute the effect sizes for the two significant correlations, because, after all, it’s important to know not only that there is a “real” effect, but also how big that effect is. When we do that, it turns out that the point-biserial correlation is huge! It’s .75 for the BDI and .68 for the ZSRDS. In other words, about half of the variance in clowndom can be explained by depression levels. And of course, because we’re well aware that correlation does not imply causation, we get to interpret the correlation both ways! So we quickly issue a press release claiming that we’ve discovered that it’s possible to conclusively diagnose depression just by knowing whether or not someone’s a clown! (We’re not going to worry about silly little things like base rates in a press release.)
Now, this may all seem great. And it’s probably not an unrealistic depiction of how much of psychology works (well, minus the colorful scarves, big hair, and face paint). That is, very often people report interesting findings that were selectively reported from amongst a larger pool of potential findings on the basis of the fact that the former but not the latter surpassed some predetermined criterion for statistical significance. For example, in our hypothetical in press clown paper, we don’t bother to report results for the correlation between clownhood and the Center for Epidemiologic Studies Depression Scale (r = .12, p > .1). Why should we? It’d be silly to report a whole pile of additional correlations only to turn around and say “null effect, null effect, null effect, null effect, null effect, null effect, null effect, and null effect” (see how boring it was to read that?). Nobody cares about variables that don’t predict other variables; we care about variables that do predict other variables. And we’re not really doing anything wrong, we think; it’s not like the act of selective reporting is inflating our Type I error (i.e., the false positive rate), because we’ve already taken care of that up front by deliberately being overconservative in our analyses.
Unfortunately, while it’s true that our Type I error doesn’t suffer, the act of choosing which findings to report based on the results of a statistical test does have another unwelcome consequence. Specifically, there’s a very good chance that the effect sizes we end up reporting for statistically significant results will be artificially inflated–perhaps dramatically so.
Why would this happen? It’s actually entailed by the selection procedure. To see this, let’s take the classical measurement model, under which the variance in any measured variable reflects the sum of two components: the “true” scores (i.e., the scores we would get if our measurements were always completely accurate) and some random error. The error term can in turn be broken down into many more specific sources of error; but we’ll ignore that and just focus on one source of error–namely, sampling error. Sampling error refers to the fact that we can never select a perfectly representative group of subjects when we collect a sample; there’s always some (ideally small) way in which the sample characteristics differ from the population. This error term can artificially inflate an effect or artificially deflate it, and it can inflate or deflate it more or less, but it’s going to have an effect one way or the other. You can take that to the bank as sure as my name’s Bozo the Clown.
To put this in context, let’s go back to our BDI scores. Recall that what we observed is that clowns have higher BDI scores than non-clowns. But what we’re now saying is that that difference in scores is going to be affected by sampling error. That is, just by chance, we may have selected a group of clowns that are particularly depressed, or a group of non-clowns who are particularly jolly. Maybe if we could measure depression in all clowns and all non-clowns, we would actually find no difference between groups.
Now, if we allow that sampling error really is random, and that we’re not actively trying to pre-determine the outcome of our study by going out of our way to recruit The Great Depressed Mancini and his extended dysthymic clown family, then in theory we have no reason to think that sampling error is going to introduce any particular bias into our results. It’s true that the observed correlations in our sample may not be perfectly representative of the true correlations in the population; but that’s not a big deal so long as there’s no systematic bias (i.e., that we have no reason to think that our sample will systematically inflate correlations or deflate them). But here’s the problem: the act of choosing to report some correlations but not others on the basis of their statistical significance (or lack thereof) introduces precisely such a bias. The reason is that, when you go looking for correlations that are of a certain size or greater, you’re inevitably going to be more likely to select those correlations that happen to have been helped by chance than hurt by it.
Here’s a series of figures that should make the point even clearer. Let’s pretend for a moment that the truth of the matter is that there is in fact a positive correlation between clown status and all 10 depression measures. Except, we’ll make it 100 measures, because it’ll be easier to illustrate the point that way. Moreover, let’s suppose that the correlation is exactly the same for all 100 measures, at .3. Here’s what that would look like if we just plotted the correlations for all 100 measures, 1 through 100:

It’s just a horizontal red line, because all the individual correlations have the same value (0.3). So that’s not very exciting. But remember, these are the population correlations. They’re not what we’re going to observe in our sample of 20 clowns and 20 non-clowns, because depression scores in our sample aren’t a perfect representation of the population. There’s also error to worry about. And error–or at least, sampling error–is going to be greater for smaller samples than for bigger ones. (The reason for this can be expressed intuitively: other things being equal, the more observations you have, the more representative your sample must be of the population as a whole, because deviations in any given direction will tend to cancel each other out the more data you collect. And if you keep collecting, at the limit, your sample will constitute the whole population, and must therefore by definition be perfectly representative). With only 20 subjects in each group, our estimates of each group’s depression level are not going to be terrifically stable. You can see this in the following figure, which shows the results of a simulation on 100 different variables, assuming that all have an identical underlying correlation of .3:
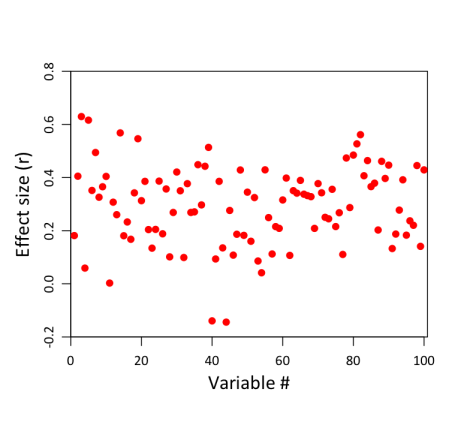
Notice how much variability there is in the correlations! The weakest correlation is actually negative, at -.18; the strongest is much larger than .3, at .63. (Caveat for more technical readers: this assumes that the above variables are completely independent, which in practice is unlikely to be true when dealing with 100 measures of the same construct.) So even though the true correlation is .3 in all cases, the magic of sampling will necessarily produce some values that are below .3, and some that are above .3. In some cases, the deviations will be substantial.
By now you can probably see where this is going. Here we have a distribution of effect sizes that to some extent may reflect underlying variability in population effect sizes, but is also almost certainly influenced by sampling error. And now we come along and decide that, hey, it doesn’t really make sense to report all 100 of these correlations in a paper; that’s too messy. Really, for the sake of brevity and clarity, we should only report those correlations that are in some sense more important and “real”. And we do that by calculating p-values and only reporting the results of tests that are significant at some predetermined level (in our case, p < .005). Well, here’s what that would look like:

This is exactly the same figure as the previous one, except we’ve now grayed out all the non-significant correlations. And in the process, we’ve made Bozo the Clown cry:
Why? Because unfortunately, the criterion that we’ve chosen is an extremely conservative one. In order to detect a significant difference in means between two groups of 20 subjects at p < .005, the observed correlation (depicted as the horizontal black line above) needs to be .42 or greater! That’s substantially larger than the actual population effect size of .3. Effects of this magnitude don’t occur very frequently in our sample; in fact, they only occur 16 times. As a result, we’re going to end up failing to detect 84 of 100 correlations, and will walk away thinking they’re null results–even though the truth is that, in the population, they’re actually all pretty strong, at .3. This quantity–the proportion of “real” effects that we’re likely to end up calling statistically significant given the constraints of our sample–is formally called statistical power. If you do a power analysis for a two-sample t-test on a correlation of .3 at p < .005, it turns out that power is only .17 (which is essentially what we see above; the slight discrepancy is due to chance). In other words, even when there are real and relatively strong associations between depression and clownhood, our sample would only identify those associations 17% of the time, on average.
That’s not good, obviously, but there’s more. Now the other shoe drops, because not only have we systematically missed out on most of the effects we’re interested in (in virtue of using small samples and overly conservative statistical thresholds), but notice what we’ve also done to the effect sizes of those correlations that we do end up identifying. What is in reality a .3 correlation spuriously appears, on average, as a .51 correlation in the 16 tests that surpass our threshold. So, through the combined magic of low power and selection bias, we’ve turned what may in reality be a relatively diffuse association between two variables (say, clownhood and depression) into a seemingly selective and extremely strong association. After all the excitement about getting a high-profile publication, it might ultimately turn out that clowns aren’t really so depressed after all–it’s all an illusion induced by the sampling apparatus. So you might say that the clowns get the last laugh. Or that the joke’s on us. Or maybe just that this whole clown example is no longer funny and it’s now time for it to go bury itself in a hole somewhere.
Anyway, that, in a nutshell, was the point my commentary on the Vul et al paper made, and it’s the same point the Gelman and Wainer papers make too, in one way or another. While it’s a very general point that really applies in any domain where (a) power is less than 100% (which is just about always) and (b) there is some selection bias (which is also just about always), there were some considerations that were particularly applicable to fMRI research. The basic issue is that, in fMRI research, we often want to conduct analyses that span the entire brain, which means we’re usually faced with conducting many more statistical comparisons than researchers in other domains generally deal with (though not, say, molecular geneticists conducting genome-wide association studies). As a result, there is a very strong emphasis in imaging research on controlling Type I error rates by using very conservative statistical thresholds. You can agree or disagree with this general advice (for the record, I personally think there’s much too great an emphasis in imaging on Type I error, and not nearly enough emphasis on Type II error), but there’s no avoiding the fact that following it will tend to produce highly inflated significant effect sizes, because in the act of reducing p-value thresholds, we’re also driving down power dramatically, and making the selection bias more powerful.
While it’d be nice if there was an easy fix for this problem, there really isn’t one. In behavioral domains, there’s often a relatively simple prescription: report all effect sizes, both significant and non-significant. This doesn’t entirely solve the problem, because people are still likely to overemphasize statistically significant results relative to non-significant ones; but at least at that point you can say you’ve done what you can. In the fMRI literature, this course of action isn’t really available, because most journal editors are not going to be very happy with you when you send them a 25-page table that reports effect sizes and p-values for each of the 100,000 voxels you tested. So we’re forced adopt other strategies. The one I’ve argued for most strongly is to increase sample size (which increases power and decreases the uncertainty of resulting estimates). But that’s understandably difficult in a field where scanning each additional subject can cost $1,000 or more. There are a number of other things you can do, but I won’t talk about them much here, partly because this is already much too long a post, but mostly because I’m currently working on a paper that discusses this problem, and potential solutions, in much more detail.
So now finally I get to the Ioannidis article. As I said, the basic point is the same one made in my paper and Gelman’s and others, and the one I’ve described above in excruciating clownish detail. But there are a number of things about the Ioannidis that are particularly nice. One is that Ioannidis considers not only inflation due to selection of statistically significant results coupled with low power, but also inflation due to the use of flexible analyses (or, as he puts it, “vibration” of effects–also known as massaging the data). Another is that he considers cultural aspects of the phenomenon, e.g., the fact that investigators tend to be rewarded for reporting large effects, even if they subsequently fail to replicate. He also discusses conditions under which you might actually get deflation of effect sizes–something I didn’t touch on in my commentary, and hadn’t really thought about. Finally, he makes some interesting recommendations for minimizing effect size inflation. Whereas my commentary focused primarily on concrete steps researchers could take in individual studies to encourage clearer evaluation of results (e.g., reporting confidence intervals, including power calculations, etc.), Ioannidis focuses on longer-term solutions and the possibility that we’ll need to dramatically change the way we do science (at least in some fields).
Anyway, this whole issue of inflated effect sizes is a critical one to appreciate if you do any kind of social or biomedical science research, because it almost certainly affects your findings on a regular basis, and has all sorts of implications for what kind of research we conduct and how we interpret our findings. (To give just one trivial example, if you’ve ever been tempted to attribute your failure to replicate a previous finding to some minute experimental difference between studies, you should seriously consider the possibility that the original effect size may have been grossly inflated, and that your own study consequently has insufficient power to replicate the effect.) If you only have time to read one article that deals with this issue, read the Ioannidis paper. And remember it when you write your next Discussion section. Bozo the Clown will thank you for it.
Ioannidis, J. (2008). Why Most Discovered True Associations Are Inflated Epidemiology, 19 (5), 640-648 DOI: 10.1097/EDE.0b013e31818131e7
Yarkoni, T. (2009). Big Correlations in Little Studies: Inflated fMRI Correlations Reflect Low Statistical Power-Commentary on Vul et al. (2009) Perspectives on Psychological Science, 4 (3), 294-298 DOI: 10.1111/j.1745-6924.2009.01127.x
more pretty pictures of brains
Google Reader‘s new recommendation engine is pretty nifty, and I find it gets it right most of the time. It just suggested this blog, which looks to be a nice (and growing) collection of neuro-related images. It’s an interesting set of pictures that go beyond the usual combination of brain slices and tractography images to include paintings of brains (and their owners) in strange poses, psychedelic posters, and abandoned Russian brain labs. For example:
In a similar vein, there’s also this, which seems to be the CNS-related incarnation of another earlier favorite.
fourteen feet of snow!!!
tuesday at 3 pm works for me
Apparently, Tuesday at 3 pm is the best time to suggest as a meeting time–that’s when people have the most flexibility available in their schedule. At least, that’s the conclusion drawn by a study based on data from WhenIsGood, a free service that helps with meeting scheduling. There’s not much to the study beyond the conclusion I just gave away; not surprisingly, people don’t like to meet before 10 or 11 am or after 4 pm, and there’s very little difference in availability across different days of the week.
What I find neat about this isn’t so much the results of the study itself as the fact that it was done at all. I’m a big proponent of using commercial website data for research purposes–I’m about to submit a paper that relies almost entirely on content pulled using the Blogger API, and am working on another project that makes extensive use of the Twitter API. The scope of the datasets one can assemble via these APIs is simply unparalleled; for example, there’s no way I could ever realistically collect writing samples of 50,000+ words from 500+ participants in a laboratory setting, yet the ability to programmatically access blogspot.com blog contents makes the task trivial. And of course, many websites collect data of a kind that just isn’t available off-line. For example, the folks at OKCupid are able to continuously pump out interesting data on people’s online dating habits because they have comprehensive data on interactions between literally millions of prospective dating partners. If you want to try to generate that sort of data off-line, I hope you have a really large lab.
Of course, I recognize that in this case, the WhenIsGood study really just amounts to a glorified press release. You can tell that’s what it is from the URL, which literally includes the “press/” directory in its path. So I’m certainly not naive enough to think that Web 2.0 companies are publishing interesting research based on their proprietary data solely out of the goodness of their hearts. Quite the opposite. But I think in this case the desire for publicity works in researchers’ favor: It’s precisely because virtually any press is considered good press that many of these websites would probably be happy to let researchers play with their massive (de-identified) datasets. It’s just that, so far, hardly anyone’s asked. The Web 2.0 world is a largely untapped resource that researchers (or at least, psychologists) are only just beginning to take advantage of.
I suspect that this will change in the relatively near future. Five or ten years from now, I imagine that a relatively large chunk of the research conducted in many area of psychology (particularly social and personality psychology) will rely heavily on massive datasets derived from commercial websites. And then we’ll all wonder in amazement at how we ever put up with the tediousness of collecting real-world data from two or three hundred college students at a time, when all of this online data was just lying around waiting for someone to come take a peek at it.




