Andrew Gelman posted a link on his blog today to a paper by John Ioannidis I hadn’t seen before. In many respects, it’s basically the same paper I wrote earlier this year as a commentary on the Vul et al “voodoo correlations” paper (the commentary was itself based largely on an earlier chapter I wrote with my PhD advisor, Todd Braver). Well, except that the Ioannidis paper came out a year earlier than mine, and is also much better in just about every respect (more on this below).
What really surprises me is that I never came across Ioannidis’ paper when I was doing a lit search for my commentary. The basic point I made in the commentary–which can be summarized as the observation that low power coupled with selection bias almost invariably inflates significant effect sizes–is a pretty straightforward statistical point, so I figured that many people, and probably most statisticians, were well aware of it. But no amount of Google Scholar-ing helped me find an authoritative article that made the same point succinctly; I just kept coming across articles that made the point tangentially, in an off-hand “but of course we all know we shouldn’t trust these effect sizes, because…” kind of way. So I chalked it down as one of those statistical factoids (of which there are surprisingly many) that live in the unhappy land of too-obvious-for-statisticians-to-write-an-article-about-but-not-obvious-enough-for-most-psychologists-to-know-about. And so I just went ahead and wrote the commentary in a non-technical way that I hoped would get the point across intuitively.
Anyway, after the commentary was accepted, I sent a copy to Andrew Gelman, who had written several posts about the Vul et al controversy. He promptly send me back a link to this paper of his, which basically makes the same point about sampling error, but with much more detail and much better examples than I did. His paper also cites an earlier article in American Scientist by Wainer, which I also recommend, and again expresses very similar ideas. So then I felt a bit like a fool for not stumbling across either Gelman’s paper or Wainer’s earlier. And now that I’ve read Ioannidis’ paper, I feel even dumber, seeing as I could have saved myself a lot of trouble by writing two or three paragraphs and then essentially pointing to Ioannidis’ work. Oh well.
That all said, it wasn’t a complete loss; I still think the basic point is important enough that it’s worth repeating loudly and often, no matter how many times it’s been said before. And I’m skeptical that many fMRI researchers would have appreciated the point otherwise, given that none of the papers I’ve mentioned were published in venues fMRI researchers are likely to read regularly (which is presumably part of the reason I never came across them!). Of course, I don’t think that many people who do fMRI research actually bothered to read my commentary, so it’s questionable whether it had much impact anyway.
At any rate, the Ioannidis paper makes a number of points that my paper didn’t, so I figured I’d talk about them a bit. I’ll start by revisiting what I said in my commentary, and then I’ll tell you why you should read Ioannidis’ paper instead of mine.
The basic intuition can be captured as follows. Suppose you’re interested in the following question: Do clowns suffer depression at a higher rate than us non-comical folk do? You might think this is a contrived (to put it delicately) question, but I can assure you it has all sorts of important real-world implications. For instance, you wouldn’t be so quick to book a clown for your child’s next birthday party if you knew that The Great Mancini was going to be out in the parking lot half an hour later drinking cheap gin out of a top hat. If that example makes you feel guilty, congratulations: you’ve just discovered the translational value of basic science.
Anyway, back to the question, and how we’re going to answer it. You can’t just throw a bunch of clowns and non-clowns in a room and give them a depression measure. There’s nothing comical about that. What you need to do, if you’re rigorous about it, is give them multiple measures of depression, because we all know how finicky individual questionnaires can be. So the clowns and non-clowns each get to fill out the Beck Depression Inventory (BDI), the Center for Epidemiologic Studies Depression Scale, the Depression Adjective Checklist, the Zung Self-Rating Depression Scale (ZSRDS), and, let’s say, six other measures. Ten measures in all. And let’s say we have 20 individuals in each group, because that’s all I personally a cash-strapped but enthusiastic investigator can afford. After collecting the data, we score the questionnaires and run a bunch of t-tests to determine whether clowns and non-clowns have different levels of depression. Being scrupulous researchers who care a lot about multiple comparisons correction, we decide to divide our critical p-value by 10 (the dreaded Bonferroni correction, for 10 tests in this case) and test at p < .005. That’s a conservative analysis, of course; but better safe than sorry!
So we run our tests and get what look like mixed results. Meaning, we get statistically significant positive correlations between clown-dom status and depression for 2 measures–the BDI and Zung inventories–but not for the other 8 measures. So that’s admittedly not great; it would have been better if all 10 had come out right. Still, it at least partially supports our hypothesis: Clowns are fucking miserable! And because we’re already thinking ahead to how we’re going to present these results when they (inevitably) get published in Psychological Science, we go ahead and compute the effect sizes for the two significant correlations, because, after all, it’s important to know not only that there is a “real” effect, but also how big that effect is. When we do that, it turns out that the point-biserial correlation is huge! It’s .75 for the BDI and .68 for the ZSRDS. In other words, about half of the variance in clowndom can be explained by depression levels. And of course, because we’re well aware that correlation does not imply causation, we get to interpret the correlation both ways! So we quickly issue a press release claiming that we’ve discovered that it’s possible to conclusively diagnose depression just by knowing whether or not someone’s a clown! (We’re not going to worry about silly little things like base rates in a press release.)
Now, this may all seem great. And it’s probably not an unrealistic depiction of how much of psychology works (well, minus the colorful scarves, big hair, and face paint). That is, very often people report interesting findings that were selectively reported from amongst a larger pool of potential findings on the basis of the fact that the former but not the latter surpassed some predetermined criterion for statistical significance. For example, in our hypothetical in press clown paper, we don’t bother to report results for the correlation between clownhood and the Center for Epidemiologic Studies Depression Scale (r = .12, p > .1). Why should we? It’d be silly to report a whole pile of additional correlations only to turn around and say “null effect, null effect, null effect, null effect, null effect, null effect, null effect, and null effect” (see how boring it was to read that?). Nobody cares about variables that don’t predict other variables; we care about variables that do predict other variables. And we’re not really doing anything wrong, we think; it’s not like the act of selective reporting is inflating our Type I error (i.e., the false positive rate), because we’ve already taken care of that up front by deliberately being overconservative in our analyses.
Unfortunately, while it’s true that our Type I error doesn’t suffer, the act of choosing which findings to report based on the results of a statistical test does have another unwelcome consequence. Specifically, there’s a very good chance that the effect sizes we end up reporting for statistically significant results will be artificially inflated–perhaps dramatically so.
Why would this happen? It’s actually entailed by the selection procedure. To see this, let’s take the classical measurement model, under which the variance in any measured variable reflects the sum of two components: the “true” scores (i.e., the scores we would get if our measurements were always completely accurate) and some random error. The error term can in turn be broken down into many more specific sources of error; but we’ll ignore that and just focus on one source of error–namely, sampling error. Sampling error refers to the fact that we can never select a perfectly representative group of subjects when we collect a sample; there’s always some (ideally small) way in which the sample characteristics differ from the population. This error term can artificially inflate an effect or artificially deflate it, and it can inflate or deflate it more or less, but it’s going to have an effect one way or the other. You can take that to the bank as sure as my name’s Bozo the Clown.
To put this in context, let’s go back to our BDI scores. Recall that what we observed is that clowns have higher BDI scores than non-clowns. But what we’re now saying is that that difference in scores is going to be affected by sampling error. That is, just by chance, we may have selected a group of clowns that are particularly depressed, or a group of non-clowns who are particularly jolly. Maybe if we could measure depression in all clowns and all non-clowns, we would actually find no difference between groups.
Now, if we allow that sampling error really is random, and that we’re not actively trying to pre-determine the outcome of our study by going out of our way to recruit The Great Depressed Mancini and his extended dysthymic clown family, then in theory we have no reason to think that sampling error is going to introduce any particular bias into our results. It’s true that the observed correlations in our sample may not be perfectly representative of the true correlations in the population; but that’s not a big deal so long as there’s no systematic bias (i.e., that we have no reason to think that our sample will systematically inflate correlations or deflate them). But here’s the problem: the act of choosing to report some correlations but not others on the basis of their statistical significance (or lack thereof) introduces precisely such a bias. The reason is that, when you go looking for correlations that are of a certain size or greater, you’re inevitably going to be more likely to select those correlations that happen to have been helped by chance than hurt by it.
Here’s a series of figures that should make the point even clearer. Let’s pretend for a moment that the truth of the matter is that there is in fact a positive correlation between clown status and all 10 depression measures. Except, we’ll make it 100 measures, because it’ll be easier to illustrate the point that way. Moreover, let’s suppose that the correlation is exactly the same for all 100 measures, at .3. Here’s what that would look like if we just plotted the correlations for all 100 measures, 1 through 100:

It’s just a horizontal red line, because all the individual correlations have the same value (0.3). So that’s not very exciting. But remember, these are the population correlations. They’re not what we’re going to observe in our sample of 20 clowns and 20 non-clowns, because depression scores in our sample aren’t a perfect representation of the population. There’s also error to worry about. And error–or at least, sampling error–is going to be greater for smaller samples than for bigger ones. (The reason for this can be expressed intuitively: other things being equal, the more observations you have, the more representative your sample must be of the population as a whole, because deviations in any given direction will tend to cancel each other out the more data you collect. And if you keep collecting, at the limit, your sample will constitute the whole population, and must therefore by definition be perfectly representative). With only 20 subjects in each group, our estimates of each group’s depression level are not going to be terrifically stable. You can see this in the following figure, which shows the results of a simulation on 100 different variables, assuming that all have an identical underlying correlation of .3:
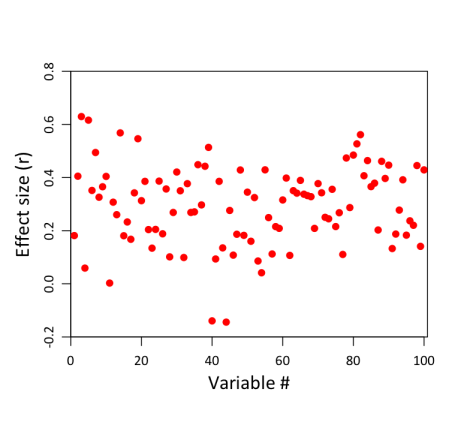
Notice how much variability there is in the correlations! The weakest correlation is actually negative, at -.18; the strongest is much larger than .3, at .63. (Caveat for more technical readers: this assumes that the above variables are completely independent, which in practice is unlikely to be true when dealing with 100 measures of the same construct.) So even though the true correlation is .3 in all cases, the magic of sampling will necessarily produce some values that are below .3, and some that are above .3. In some cases, the deviations will be substantial.
By now you can probably see where this is going. Here we have a distribution of effect sizes that to some extent may reflect underlying variability in population effect sizes, but is also almost certainly influenced by sampling error. And now we come along and decide that, hey, it doesn’t really make sense to report all 100 of these correlations in a paper; that’s too messy. Really, for the sake of brevity and clarity, we should only report those correlations that are in some sense more important and “real”. And we do that by calculating p-values and only reporting the results of tests that are significant at some predetermined level (in our case, p < .005). Well, here’s what that would look like:

This is exactly the same figure as the previous one, except we’ve now grayed out all the non-significant correlations. And in the process, we’ve made Bozo the Clown cry:
Why? Because unfortunately, the criterion that we’ve chosen is an extremely conservative one. In order to detect a significant difference in means between two groups of 20 subjects at p < .005, the observed correlation (depicted as the horizontal black line above) needs to be .42 or greater! That’s substantially larger than the actual population effect size of .3. Effects of this magnitude don’t occur very frequently in our sample; in fact, they only occur 16 times. As a result, we’re going to end up failing to detect 84 of 100 correlations, and will walk away thinking they’re null results–even though the truth is that, in the population, they’re actually all pretty strong, at .3. This quantity–the proportion of “real” effects that we’re likely to end up calling statistically significant given the constraints of our sample–is formally called statistical power. If you do a power analysis for a two-sample t-test on a correlation of .3 at p < .005, it turns out that power is only .17 (which is essentially what we see above; the slight discrepancy is due to chance). In other words, even when there are real and relatively strong associations between depression and clownhood, our sample would only identify those associations 17% of the time, on average.
That’s not good, obviously, but there’s more. Now the other shoe drops, because not only have we systematically missed out on most of the effects we’re interested in (in virtue of using small samples and overly conservative statistical thresholds), but notice what we’ve also done to the effect sizes of those correlations that we do end up identifying. What is in reality a .3 correlation spuriously appears, on average, as a .51 correlation in the 16 tests that surpass our threshold. So, through the combined magic of low power and selection bias, we’ve turned what may in reality be a relatively diffuse association between two variables (say, clownhood and depression) into a seemingly selective and extremely strong association. After all the excitement about getting a high-profile publication, it might ultimately turn out that clowns aren’t really so depressed after all–it’s all an illusion induced by the sampling apparatus. So you might say that the clowns get the last laugh. Or that the joke’s on us. Or maybe just that this whole clown example is no longer funny and it’s now time for it to go bury itself in a hole somewhere.
Anyway, that, in a nutshell, was the point my commentary on the Vul et al paper made, and it’s the same point the Gelman and Wainer papers make too, in one way or another. While it’s a very general point that really applies in any domain where (a) power is less than 100% (which is just about always) and (b) there is some selection bias (which is also just about always), there were some considerations that were particularly applicable to fMRI research. The basic issue is that, in fMRI research, we often want to conduct analyses that span the entire brain, which means we’re usually faced with conducting many more statistical comparisons than researchers in other domains generally deal with (though not, say, molecular geneticists conducting genome-wide association studies). As a result, there is a very strong emphasis in imaging research on controlling Type I error rates by using very conservative statistical thresholds. You can agree or disagree with this general advice (for the record, I personally think there’s much too great an emphasis in imaging on Type I error, and not nearly enough emphasis on Type II error), but there’s no avoiding the fact that following it will tend to produce highly inflated significant effect sizes, because in the act of reducing p-value thresholds, we’re also driving down power dramatically, and making the selection bias more powerful.
While it’d be nice if there was an easy fix for this problem, there really isn’t one. In behavioral domains, there’s often a relatively simple prescription: report all effect sizes, both significant and non-significant. This doesn’t entirely solve the problem, because people are still likely to overemphasize statistically significant results relative to non-significant ones; but at least at that point you can say you’ve done what you can. In the fMRI literature, this course of action isn’t really available, because most journal editors are not going to be very happy with you when you send them a 25-page table that reports effect sizes and p-values for each of the 100,000 voxels you tested. So we’re forced adopt other strategies. The one I’ve argued for most strongly is to increase sample size (which increases power and decreases the uncertainty of resulting estimates). But that’s understandably difficult in a field where scanning each additional subject can cost $1,000 or more. There are a number of other things you can do, but I won’t talk about them much here, partly because this is already much too long a post, but mostly because I’m currently working on a paper that discusses this problem, and potential solutions, in much more detail.
So now finally I get to the Ioannidis article. As I said, the basic point is the same one made in my paper and Gelman’s and others, and the one I’ve described above in excruciating clownish detail. But there are a number of things about the Ioannidis that are particularly nice. One is that Ioannidis considers not only inflation due to selection of statistically significant results coupled with low power, but also inflation due to the use of flexible analyses (or, as he puts it, “vibration” of effects–also known as massaging the data). Another is that he considers cultural aspects of the phenomenon, e.g., the fact that investigators tend to be rewarded for reporting large effects, even if they subsequently fail to replicate. He also discusses conditions under which you might actually get deflation of effect sizes–something I didn’t touch on in my commentary, and hadn’t really thought about. Finally, he makes some interesting recommendations for minimizing effect size inflation. Whereas my commentary focused primarily on concrete steps researchers could take in individual studies to encourage clearer evaluation of results (e.g., reporting confidence intervals, including power calculations, etc.), Ioannidis focuses on longer-term solutions and the possibility that we’ll need to dramatically change the way we do science (at least in some fields).
Anyway, this whole issue of inflated effect sizes is a critical one to appreciate if you do any kind of social or biomedical science research, because it almost certainly affects your findings on a regular basis, and has all sorts of implications for what kind of research we conduct and how we interpret our findings. (To give just one trivial example, if you’ve ever been tempted to attribute your failure to replicate a previous finding to some minute experimental difference between studies, you should seriously consider the possibility that the original effect size may have been grossly inflated, and that your own study consequently has insufficient power to replicate the effect.) If you only have time to read one article that deals with this issue, read the Ioannidis paper. And remember it when you write your next Discussion section. Bozo the Clown will thank you for it.
Ioannidis, J. (2008). Why Most Discovered True Associations Are Inflated Epidemiology, 19 (5), 640-648 DOI: 10.1097/EDE.0b013e31818131e7
Yarkoni, T. (2009). Big Correlations in Little Studies: Inflated fMRI Correlations Reflect Low Statistical Power-Commentary on Vul et al. (2009) Perspectives on Psychological Science, 4 (3), 294-298 DOI: 10.1111/j.1745-6924.2009.01127.x
